shining sand

This is a blog post based on a transcript of a talk Devine gave at Handmade Seattle on November 26th 2024. Watch the video version(on YouTube). The slideshow presentation was made using Adelie. A big thank you to Abner Coimbre for organizing this event.
A Shining Place Built Upon The Sand
I dreamt I was in a Library, but it didn't look like a library at all. You know how in dreams you feel like you know someone to be a specific person without them necessarily having their appearance? This is how I knew this was a library.
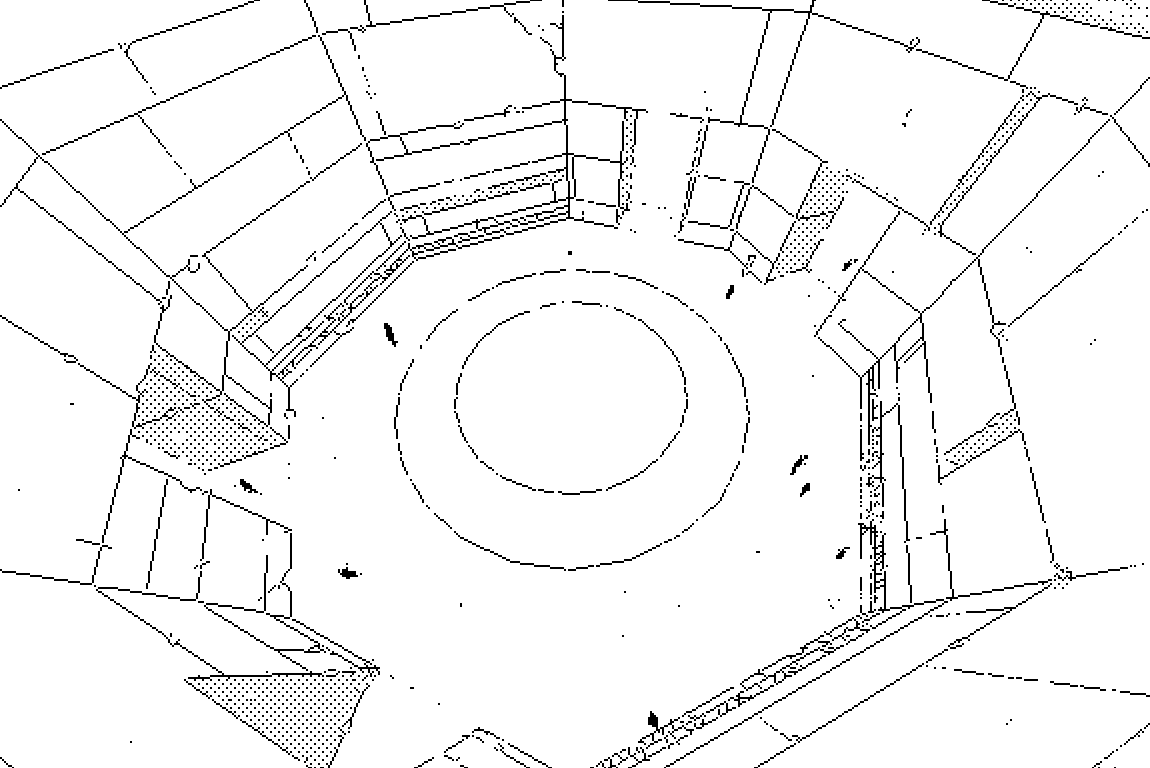
Not that this mattered to most people in it, as it was more of a backdrop to their lives, in fact, most people didn't pick up a single book in their lifetimes. Their lives were spent within the walls of large octagonal rooms. Each room had 4 hallways connecting to other rooms. Restrooms, bedrooms, and other facilities were found in the gaps. Perpetual daylight radiated from the translucent glassy floor. At the center of some octagons grew fruit trees.
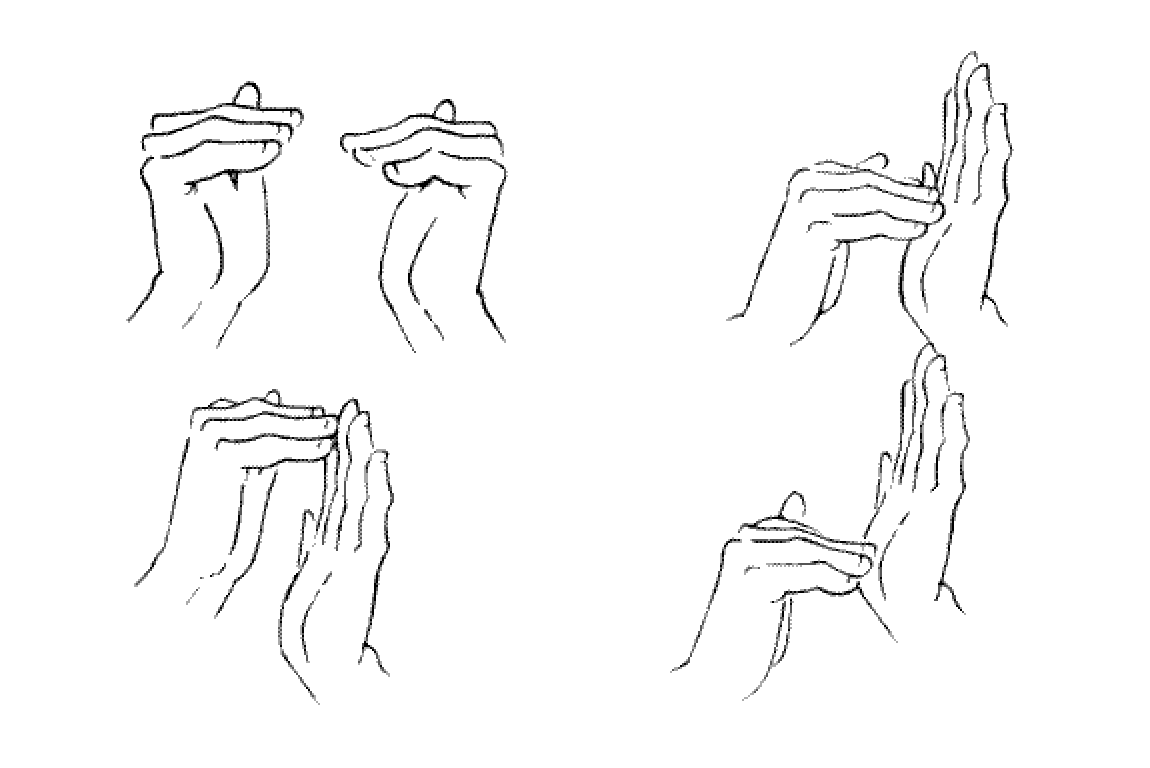
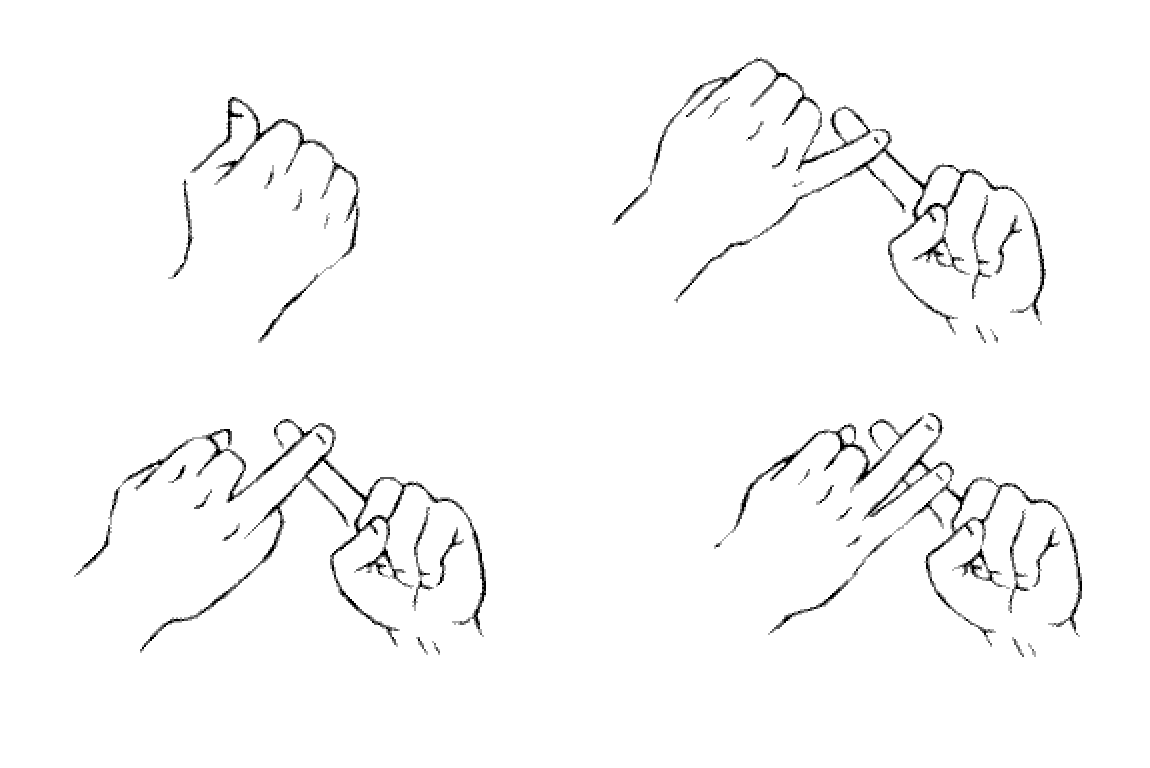
In the silence of the library, people communicated by signing to each other. Every conceivable meaning was communicated quietly that way. Each sign corresponded to either one of 32 words, or one of 16 numbers. The children learned to count with their fingers, only they counted in base-16, or in hexadecimal. They'd say that in a hand there were 4 fingers and a thumb. Each hand could count to 16, 32 if they included the thumb. Using both hands permitted counting to 256.
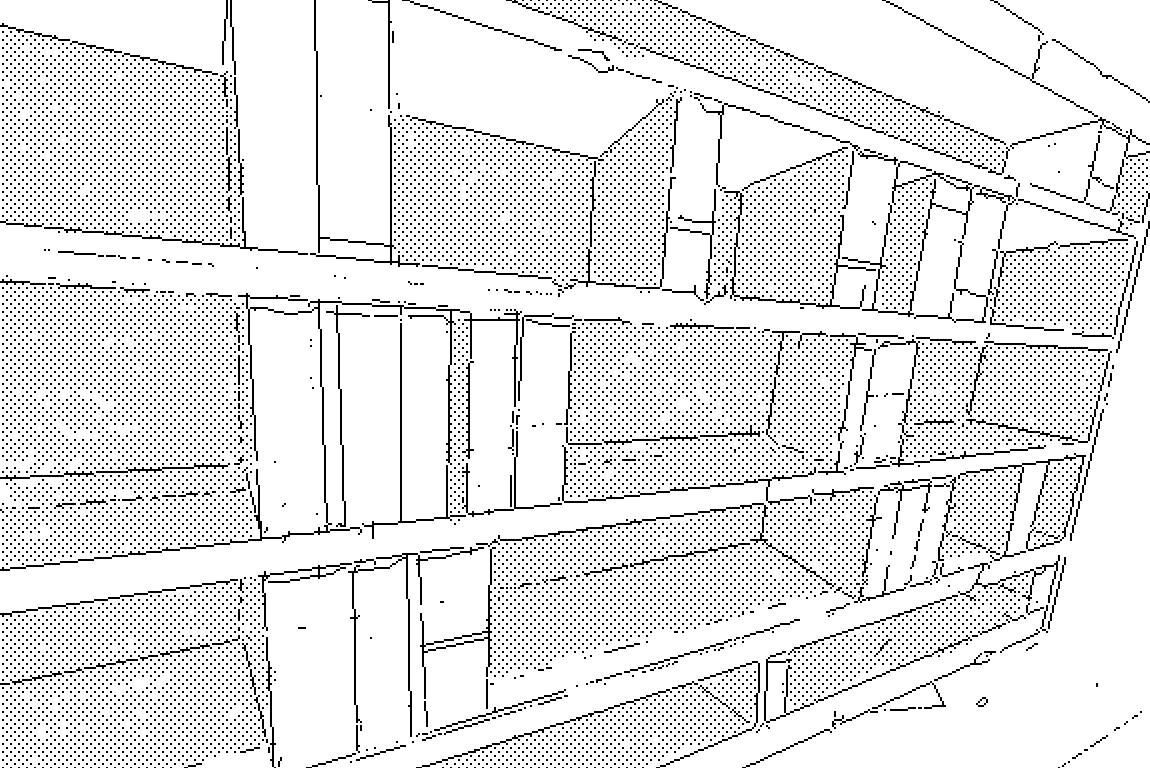
In each octagon, 4 of the walls each bore 8 shelves. Borges' books had 410 pages, each page was 40 lines long, and each line spanned 80 characters, but the books in this particular library were perfectly square, each page was 16 lines long, each line was 16 letters wide, and each book contained exactly 256 pages.

The pages were made of a material that felt like bark, on it grew a kind of moss, with which a writer could mark with a reed and erase by rubbing their thumb over the marks, like how it is possible to draw on some carpets and erase the drawings by passing a hand the other way to realign the fibers.
In my dream, the alphabet used the following 32 letters. You do not need to learn these characters, I won't be teaching you a new language, I will only show you some of its attributes.

The language has 16 numbers.

Its alphabet has some properties that you'll find in some natural languages, where letters are equivalent to numbers, and vice versa.

Unlike the latin alphabet, in which most organizations of letters are meaningless.

Or, sometimes intelligible, but equally meaningless.

Every combination of letters of this alphabet means something.

Therefore, misplacing a single letter throws the story into an entirely different direction.

Whereas, in natural languages, a wrong letter, or a shuffled word, might still preserve some of its meaning, making natural languages more robust.

The language's grammar departs from that of natural languages, in that the same line might be read multiple times. It's common to read a sentence that says to read that same line once again. It's also common to be told to skip everything until the end, only to come back. The text carries the reader to different places in the book. For example, here it says to read this 5 five times:

When coming across a word like infinity, instead of reading it infinitely, some lazy readers merely understand the word to mean infinity.
In these seemingly infinite recursions, many spend their entire lives going in circles, expecting to someday reach the book's end, even though it might not end. And so, you find them going round and round in their book, hoping to get to the end, while there is no clear process of elimination that will tell you if a book will end or not. Some books are so convoluted that people still believe that they might terminate, but they can never be sure.
For example, the snippet of text above is also known as the tak() function.
Let me show you what this does in a familiar language:
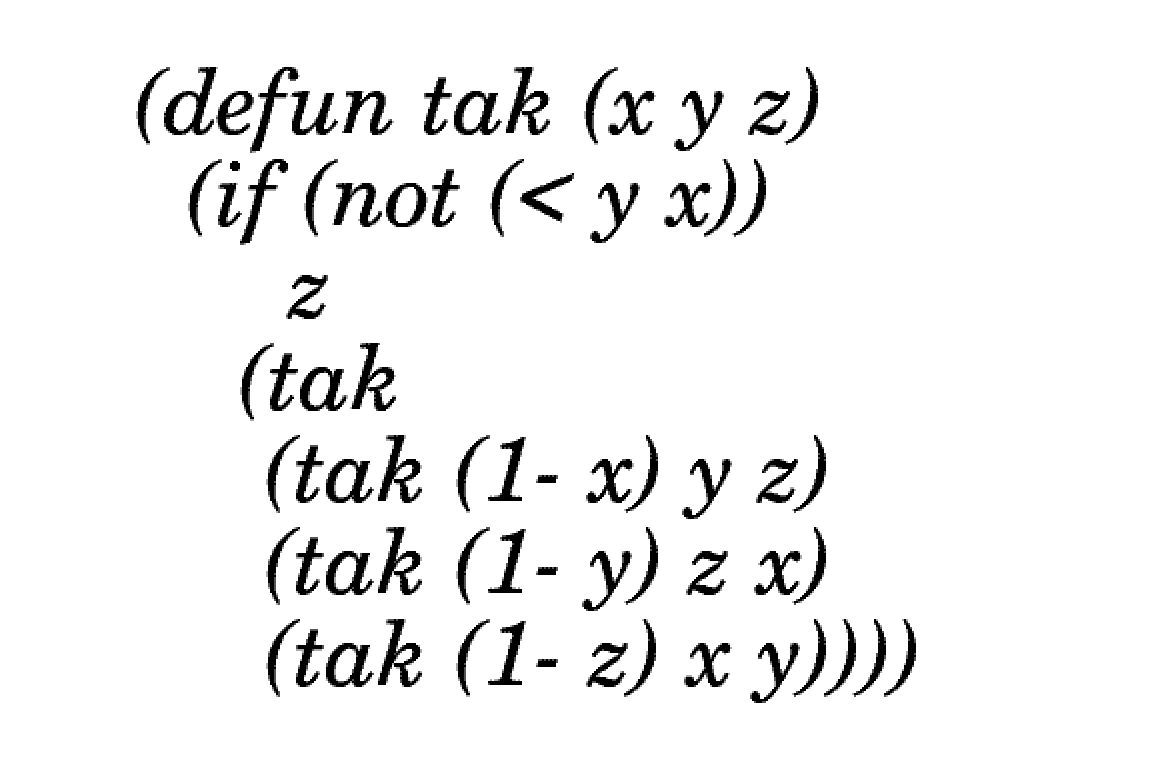
You can now understand how this sentence has consumed a lot of reading time, confounding the reader to recurse near infinitely back over the same passages.
Here is a fragment of a book which one can read in both directions, in which every letter is read(not jumped over) and just so happens to reveal the letters "T E N E T" in ASCII values.
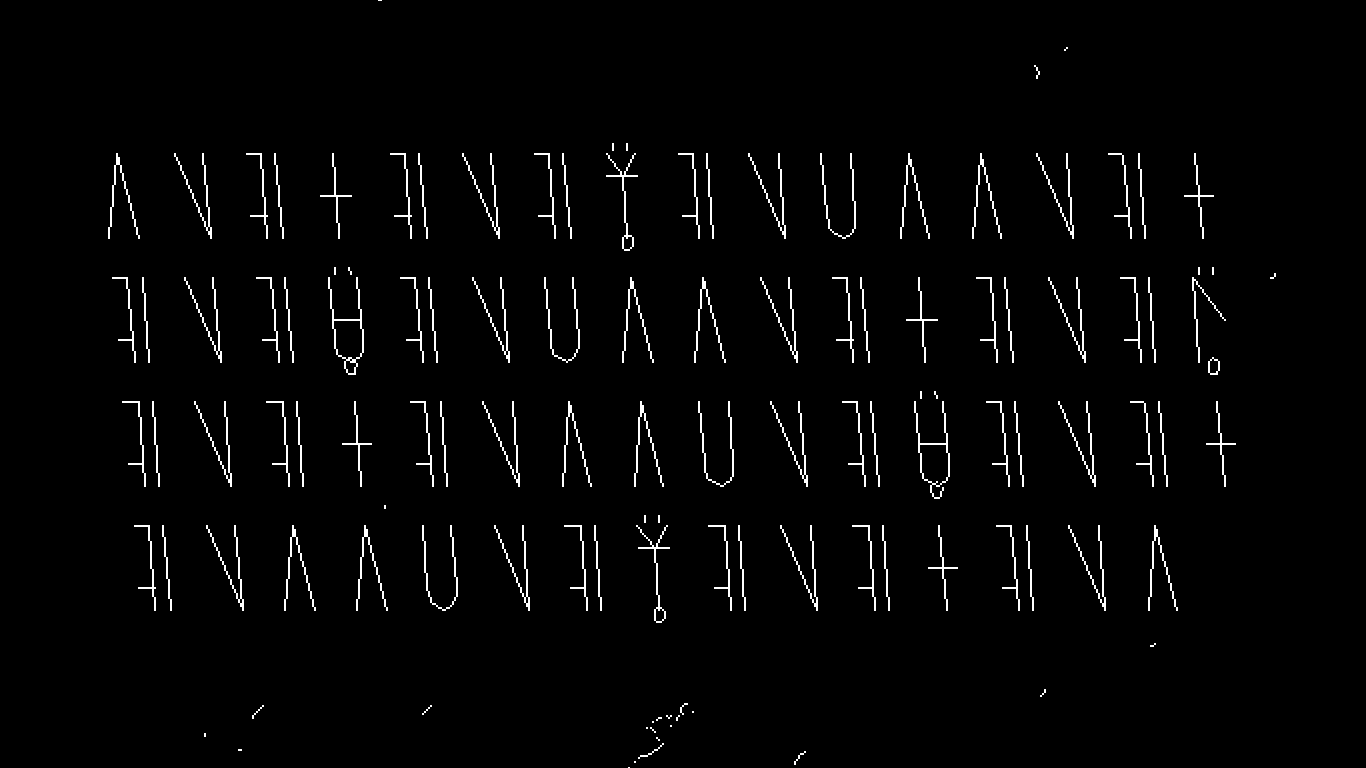
Notice how this program begins and ends with the same letter. This is called a palindromic program. Some suggested that reading the books forward and backward reduced the search for meaningful books by half. While others have said that instead, this doubles the work of searching for meaningful books because of the fear of coming across The Book, only to now fear having read it the wrong way around.
Some inhabitants of the library believed that the astronomical number of permutations of these 65536-letters books were too few, that the books didn't have enough pages, that the alphabet had too few letters.
"Get with the times!" We need bigger books!" They'd say.
"We haven't even begun to explore this one, and you want a bigger one?" I'd say, but, even in my dream, I had in my mind the idea that other libraries must exist where the symbols on the pages were different.
And others believed in the opposite, that our usage of so many characters was frivolous. They suggested that the alphabet could be encoded entirely in two characters, a dot and a dash, capable of encoding all possible meaning. So, why write this complex thing...
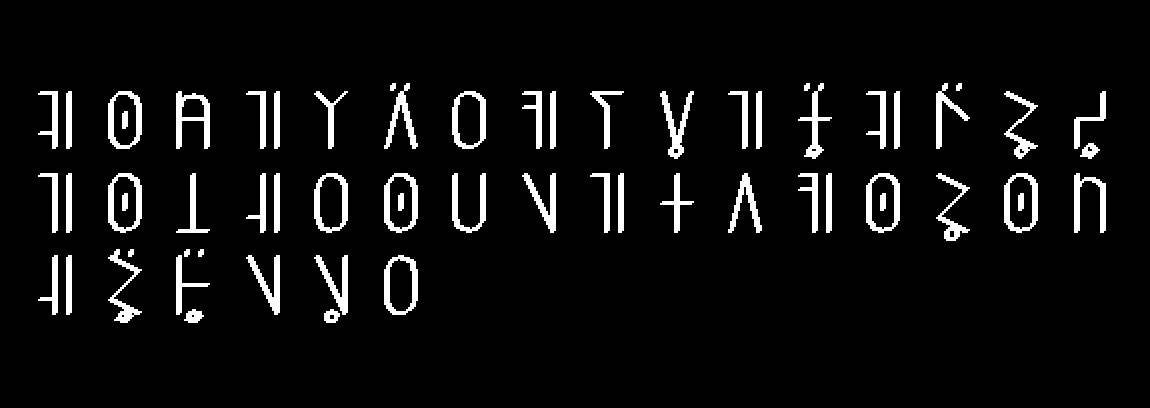
... when you can simply write this!

And so, in the library, dialects had emerged where might people use restricted sets of letters.

In fact, in my dream, after wandering the halls for what seemed a long time, I found an ancient stairway that led me downward closer to the sun. As I was going down, my fingers traced along the walls, and I noticed the brickwork began to change, it appeared that my familiar library was a rather new construction, built on top of a much older foundation. There, I met an inhabitant of the sublevels of the library. This person, whom for some reason evoked in me a sense of loss, told me that the only letters anyone needed was those 4. I was incredulous at first, it took me a while to understand what this person meant, so let me try to explain what I was told:
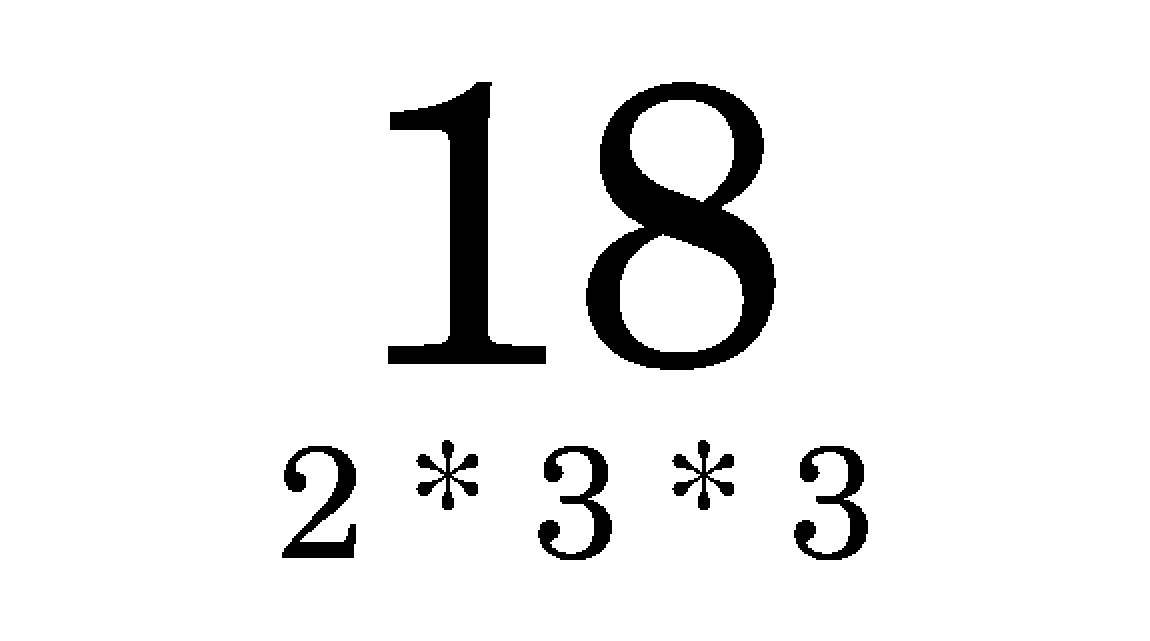
I will use decimal numbers from now on so I can communicate this to you more clearly. To understand what I'm about to tell you, it's important to understand that: the prime factoring of a number is to break it down into indivisible parts.
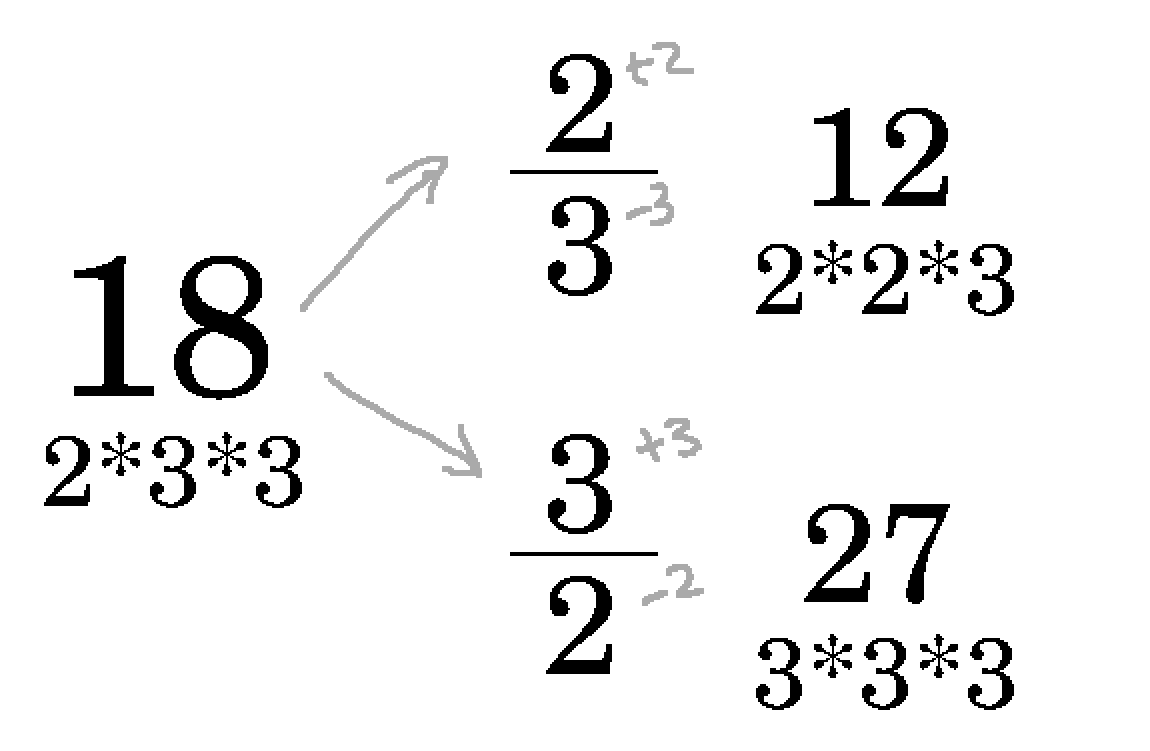
When you multiply a number by a fraction, what you're really doing is decrementing the prime factors in the denominator, and incrementing those in the numerator. For example: we remove one amount of 2 and add one amount of 3, in 3/2. We remove one amount of 3 and add one amount of 2, in 2/3.

So, we can think of any number as a bag, containing items of different numerical values, or prime values. Primes are like the DNA of numbers. These books begins with an initial number, or bag, followed by a series of fractions.
Keeping that initial number in mind, we walk through each fraction on the page. If the modulo of our accumulator and the denominator of a fraction is zero, we update our accumulator by the product of our accumulator and the fraction, and start over at the first fraction, otherwise we try the next fraction.
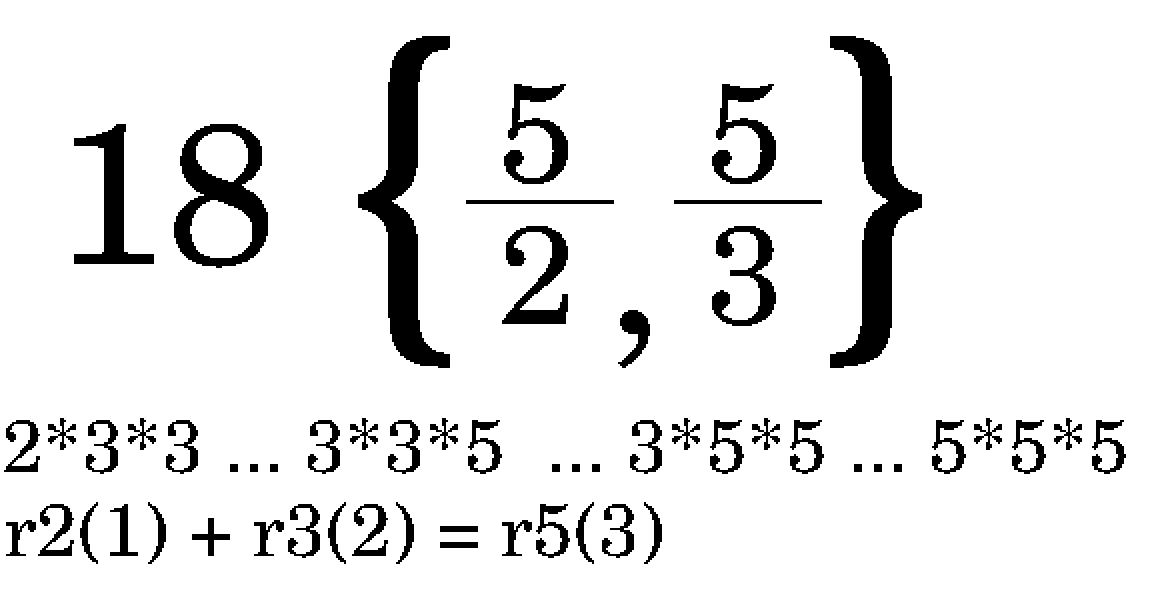
For example: (18 % 2) = 0 means that the bag is divisible by the first fraction, that our bag contains that item. We multiply 18 by 5, update the accumulator and start over until it fails to match, then move onto the second fraction, and stop upon reaching the end. This page of a book adds two numbers together stored in r2 and r3: We iterate like this, first emptying r2 into r5 Then r3 into r5. We have added 1+2=3
If we look at complete implementation of this program in pseudocode:

This is how I came to learn that each book in each library can be encoded in nothing but fractions and multiplications. But anyways, this is all too complicated, let's look at it another way. Basically, what we have on the pages is a list of changes. We can give names to registers and do away with fractions altogether: r2 = apple, r3 = orange, ..
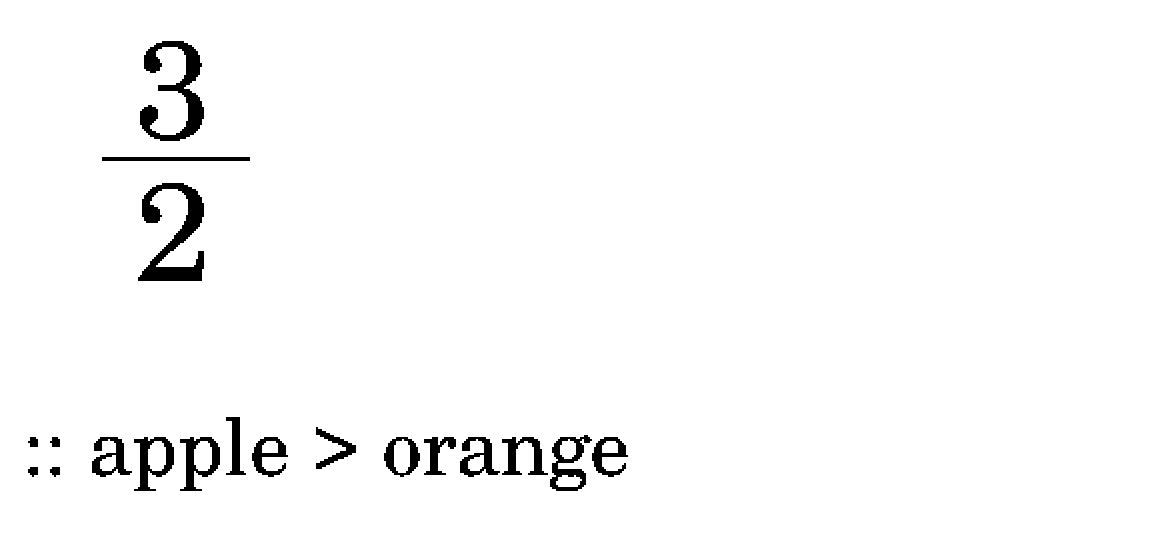
This one indicates to take an apple(r2) out of a bag, and put in two orange(r3):
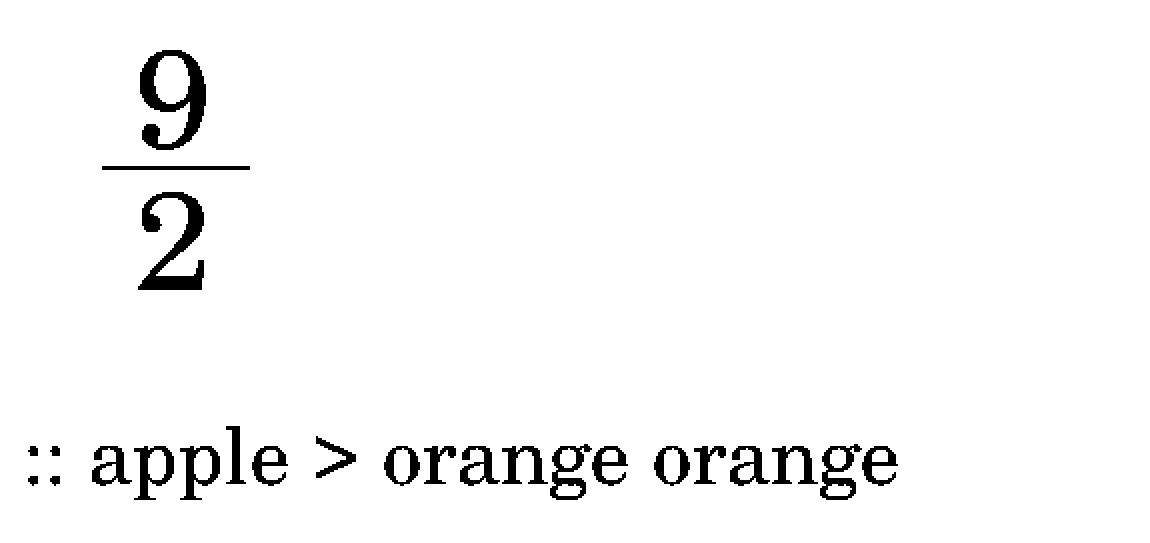
If we look at the page from before, we can think of it as these changes:
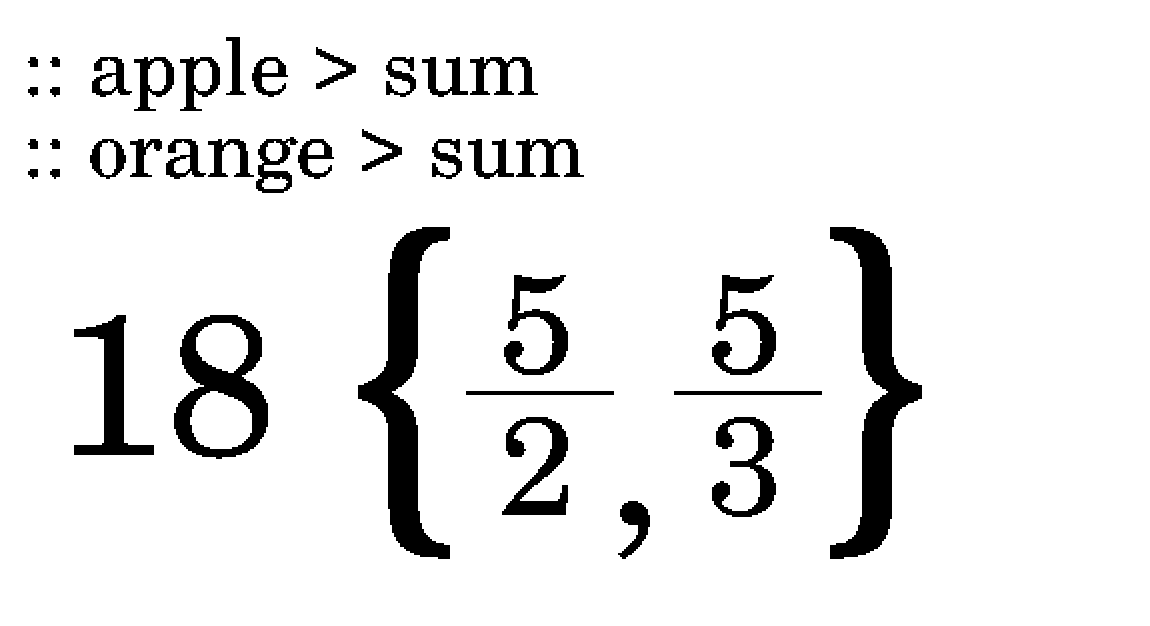
I'm using names for registers, but I could just as easily use shapes, colors, tastes, smells..
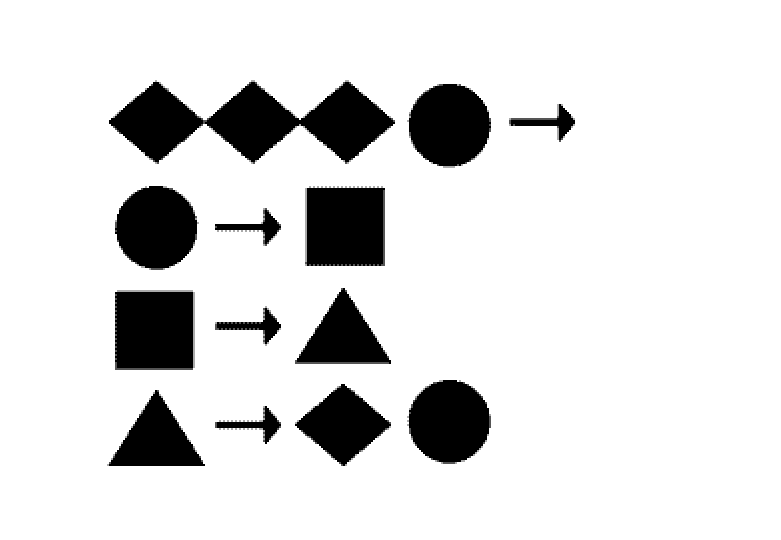
Here's what boolean logic looks like: If my bag contains the items x and y, I take them out, and put in a true item -- otherwise a false one.
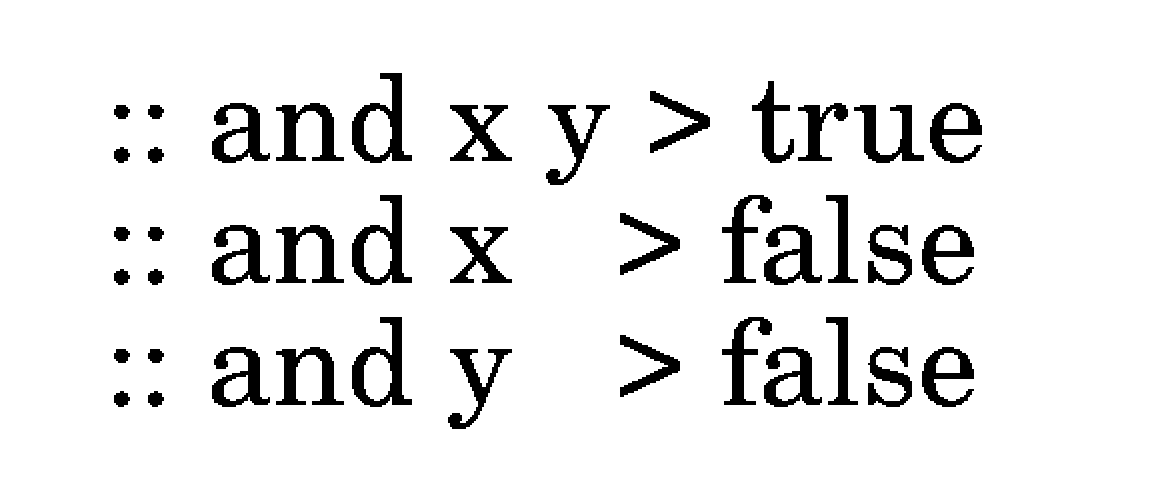
If we want to compare the value of two registers:
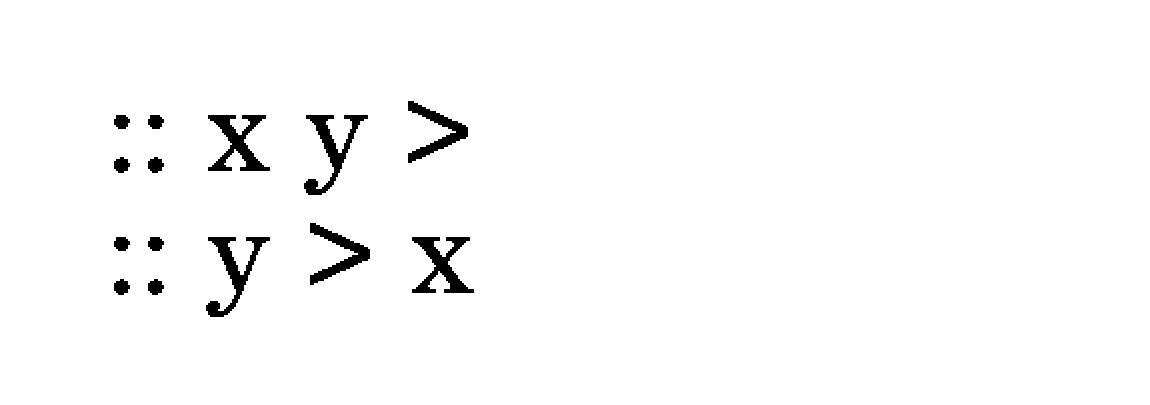
To get a Fibonacci number:

These books are reversible too, as long as the numerators and denominators are all unique. It's possible to read books backward, from the end to the start, and recover the original state — I think this is fantastic!

Beholding all these possibilities, the mind reels, the implications of a computation system so fundamental that one can explain it in 10 seconds? It transcends language, it seems to be weaved in the fabric of the universe itself! Why isn't this more known? We should rewrite our library! I'm dying to see the library halls that hold these books! I would love to see all the different libraries!
So, I asked. "Are there halls without books?"
"Yes, there are halls where the people destroyed them."
"What?! Why would anyone do that? It's inconceivable! It's painful enough to think of those who don't ever pick a book from the shelf. If it was up to me, everyone should be forced to learn how to read, a book in every hand!"
The person raised a single finger, I stopped talking.
"Why do you think the first person took one of these books off the shelf?"
"I don't know, maybe they were looking to better understand the universe, to learn about history, or just to waste some time reading some fiction." I answered.
"No, it was so they could make certain they could kill someone at a distance."
Then I woke up. Um, dreams are silly like that...
It seems I fell asleep in front of my terminal, waiting for the ARM architecture manual to open.

And, it's still loading...

For some additional context for this talk, watch the Q&A.
Thank you for reading.